www.votruba.in
Dvojková soustava a počítače
Co to je dvojková soustava?
Historie zápisu čísel a římské číslice
S vývojem poznání a rozvojem společnosti rostla i potřeba zaznamenávat. A s ní i potřeba zapisovat čísla. Různé národy v různých dobách to řešily různě. Například Římané používali následující číselnou soustavu:
| Dnešní číslice | Římské číslice |
|---|---|
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
| 5 | V |
| 9 | IX |
| 10 | X |
| 50 | L |
| 100 | C |
| 500 | D |
| 1000 | M |
V jiných dobách a zemích se používaly z roztodivných důvodů jiné soustavy - šedesátkové, dvanáctkové. Více o různých číselných soustavách a historii matematiky zde. A v Indii, odkud převzali číslice Arabové a po nich my, se začala používat tzv. poziční desítková soustava, z počátku bez nuly, od 7. století i s nulou. V této soustavě jste se učili počítat na základní škole a má řadu výhod.
Desítková a jiné poziční soustavy
Řády - zastupují mocniny základu soustavy. U desítkové soustavy mluvíme o jednotkách, desítkách, stovkách, tisících, desetitisících, ...
Číslice - vyjadřují počty od nulového k o jedna menšímu než je základ soustavy,
desítková soustava má číslice 0, 1, 2, 3, 4, 5, 6, 7, 8, 9;
osmičková soustava - 0, 1, 2, 3, 4, 5, 6, 7;
šestnáctková soustava - 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A (potřebuje číslici pro 10), B, C, D, E, F;
dvojková soustava - 0, 1 (1. výhoda - má málo číslic)
V desítkové soustavě číslo 571357 čteme pětset (tisíc) sedmdesát (tisíc) jedna tisíc třista padesát sedm, což se dá napsat 5.105+7.104+1.103+3.102+5.101+7.100
Číslo zapsané ve dvojkové soustavě 101101 by se do desítkové "přeložilo" jako 1.25+0.24+1.23+1.22+0.21+1.20=1.32+0.16+1.8+1.4+0.2+1.1=32+8+4+1=45 (1. zdánlivá nevýhoda - potřebujeme hodně mocnin dvojky k zápisu celkem malého čísla)
Převody z dvojkové do desítkové soustavy a obráceně
Čísla ze dvojkové soustavy už převádět umíme, stačí místo 1 doplnit příslušnou mocninu dvojky, počítano od 20 na posledním místě. Doporučuji mnemotechnickou pomůcku - na prstech rukou si přeříkávat mocniny dvojky: 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024; a pamatovat si 20=1.
Tím pádem číslo 1101011 můžeme rychleji převést takto: 64+32+8+2+1=107
Úkol č. 1 Převeďte do desítkové soustavy čísla 11111, 10101010, 1011001, 110011, 11110000.
Pro převod z desítkové soustavy potřebujeme postupovat obráceně: zadané číslo rozložit na součet mocnin čísla dva. Například 107=64+32+8+2+1.
Jenže co když to číslo jsme ještě nepoužili a nevidíme, jak ho rozložit?
- Najdeme nejbližší nižší mocninu čísla dva a zapíšeme 1
- Mocninu od zadaného čísla odečteme a zkontrolujeme, zda jsme další mocninu čísla dva nevynechali
- Pokud jsme mocninu čísla dva vynechali, pak za každou z nich zapíšeme 0
- Postup pokračujeme od bodu 1, dokud nezbývá nula nebo jedna, to zapíšeme na konec.
Zkusme to na číslu 129.
| Nejbližší nižší mocnina je 128 | Zapíšeme 1 |
| Odečteme 129-128=1 a kontrolujeme vynechané mocniny | 1 |
| Za vynechanou mocninu 64 zapíšeme 0 | 10 |
| Za vynechanou mocninu 32 zapíšeme 0 | 100 |
| Za vynechanou mocninu 16 zapíšeme 0 | 1000 |
| Za vynechanou mocninu 8 zapíšeme 0 | 10000 |
| Za vynechanou mocninu 4 zapíšeme 0 | 100000 |
| Za vynechanou mocninu 2 zapíšeme 0 | 1000000 |
| A zbývá nám jednička, kterou zapíšeme na konec | 10000001 |
Zkusme to na číslu 78.
| Nejbližší nižší mocnina je 64 | Zapíšeme 1 |
| Odečteme 78-64=14 a kontrolujeme vynechané mocniny | 1 |
| Za vynechanou mocninu 32 zapíšeme 0 | 10 |
| Za vynechanou mocninu 16 zapíšeme 0 | 100 |
| Další je na řadě 8, 14-8=6, zapíšeme 1 | 1001 |
| Další je na řadě 4, 6-4=2, zapíšeme 1 | 10011 |
| Další je na řadě 2, 2-2=0, zapíšeme 1 | 100111 |
| A zbývá nám nula, kterou zapíšeme na konec | 1001110 |
Úkol č. 2 Převeďte do dvojkové soustavy čísla 511, 149, 27, 151.
Existuje jiný postup? Ano, dá se postup zjednodušit tím, že číslo budeme dělit 2 a zaznamenávat si zbytky, buď 0 nebo 1. Takže si to ukažme znovu na číslu 129:
| Dělenec | Zbytek |
|---|---|
| 129 | dělíme 2 a zapíšeme zbytek |
| 64 | 1 |
| 32 | 0 |
| 16 | 0 |
| 8 | 0 |
| 4 | 0 |
| 2 | 0 |
| 1 | 0 |
| sepíšeme | 1 |
Číslo čteme odspoda nahoru: 100000012.
A zkusme znovu 78:
| Dělenec | Zbytek |
|---|---|
| 78 | dělíme 2 a zapíšeme zbytek |
| 39 | 0 |
| 19 | 1 |
| 9 | 1 |
| 4 | 1 |
| 2 | 0 |
| 1 | 0 |
| sepíšeme | 1 |
Číslo čteme odspoda nahoru: 10011102.
Úkol č. 3 Převeďte do dvojkové soustavy čísla 748, 164, 127, 51.
Jak se počítá ve dvojkové soustavě?
Teď se konečně dostaneme k tomu, proč je dvojková soustava tak výhodná - počítá se v ní totiž velmi jednoduše.
Sčítání ve dvojkové soustavě
0+0=0; 0+1=1; 1+1=10
Sčítání je komutativní, 0+1=1+0=1
Sčítání je asociativní, (0+1)+1=0+(1+1)=10
 | |
| sčítáme tak, že sečteme číslice na posledním místě: 1+0=1, nic se nepřenáší |  |
| pokračujeme na předposledním místě: 0+0=0, nic se nepřenáší | 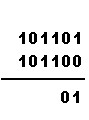 |
| a pokračujeme dál: 1+1=10, 0 zapíšeme a 1 se přenáší | 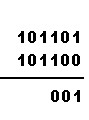 |
| přenesená 1 se přičte k 1+1, tedy 1+1+1=11, 1 se zapíše a 1 se přenáší | 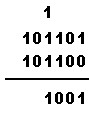 |
| přenesená 1 se přičte k 0+0, tedy 1+0+0=1, 1 se zapíše a nic se nepřenáší | 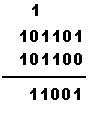 |
| 1+1=10, 0 se zapíše a 1 se přenáší | 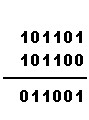 |
| zapíšeme 1 a máme výsledek |  |
101101+101100=1011001
Úkol č. 4 Sečtěte čísla: 1011+1010; 11001100+10101010; 11111+1.
Násobení ve dvojkové soustavě
0.0=0; 0.1=0; 1.1=1
Násobení je komutativní, 0.1=1.0=0
Násobení je asociativní, (0.1).1=0.(1.1)=0
Zatím asi ještě není vidět, jak je násobení jednoduché. A někomu nestačí uvědomit si, že vynásobit 0 znamená číslo "vynulovat", vynásobit 1 znamená číslo opsat. Vynásobit 10 tedy znamená, že se číslo vynásobí 0 (=0) a vynásobí 1 a v zápisu posune o řád. Výsledek se sečte => výsledkem je původní číslo, které má na konci navíc 0!. Ještě není jasné? Tak několik příkladů:
 |  |  |
Úkol č. 5 Vynásobte čísla: 110011.100; 110011.1010; 110101.1100
Distributivní zákon
Spojení násobení a sčítání: a.(b+c)=a.b+a.c
0.(0+0)=0.0+0.0=0 nebo 0.(0+0)=0.0=0
0.(0+1)=0.0+0.1=0 nebo 0.(0+1)=0.1=0
0.(1+1)=0.1+0.1=0 nebo 0.(1+1)=0.10=0
1.(0+0)=1.0+1.0=0 nebo 1.(0+0)=1.0=0
1.(0+1)=1.0+1.1=1 nebo 1.(0+1)=1.1=1
1.(1+1)=1.1+1.1=10 nebo 1.(1+1)=1.10=10
Výsledky
Úkol č. 1
31; 170; 79; 51; 240
Úkol č. 2
11111111; 10010101;11011; 110011; 10010111
Úkol č. 3
1011101100; 10100100; 1111111; 110011
Úkol č. 4
10101; 101110110; 10000
Úkol č. 5
11001100; 111111110; 1001111100